|
Kinderen iets leren wat ze nog niet weten maar waar ze wel aan toe zijn |
Worden hoogintelligente kinderen alleen geboren uit hoogintelligente ouders?Het korte antwoord luidt: bijlange niet! De grootste groep kinderen met een hoog IQ heeft ouders die zelf dichter bij het gemiddelde (IQ=100) zitten. De kans dat een ouder zelf een hoog IQ heeft, hangt wel af van de hoogte van het IQ van het kind: hoe hoger het IQ van een kind, hoe groter de kans dat de ouders een IQ boven 130 hebben. Een paar voorbeelden maken dit duidelijk:
Wat is hiervan het belang?Het is van het grootste belang dat leerkrachten hiervan op de hoogte zijn. Als leerkrachten enkel op basis van wat ze (menen te) weten over de ouders inschatten wat het mogelijke potentieel van de kinderen is, dan zullen zij bij de overgrote meerderheid van de hoogbegaafde kinderen dat potentieel veel te laag inschatten of zelfs betwisten.
Het kan wel nuttig zijn om rekening te houden met de thuisomgeving nadat je bv. vastgesteld hebt (bv. met een LVS toets boven niveau, zoals uiteengezet in het stappenplan) dat een kind een serieuze voorsprong heeft. Als een kind zo'n voorsprong opgebouwd heeft ondanks de weinig stimulerende thuissituatie, dan kun je gerust stellen dat dit kind bovengemiddelde capaciteiten heeft! Rosenthal en Jacobson (Engels) zijn bekend om hun experiment waarbij aan een groep leraren werd verteld dat één klas samengesteld was uit meer begaafde leerlingen terwijl een andere klas uit minder begaafde leerlingen bestond. In werkelijkheid was er tussen de klassen geen verschil in begaafdheid. Aan het einde van het schooljaar presteerden de leerlingen uit de 'slimme' klas beter dan die uit de 'minder slimme' klas ondanks gelijke vaardigheden en capaciteiten. Blijkbaar werden de prestaties van de leerlingen beïnvloed door de verwachtingen van de leraren. Zie Het Effect van de Glazen Bol (Klasse voor Leerkrachten nr. 50) voor nog andere voorbeelden van het belang van de verwachtingen van een leerkracht voor een leerling. Maar ook ouders dienen zich hiervan bewust te zijn. Hoogintelligente ouders moeten beseffen dat de kans heel groot is, dat hun kinderen weliswaar slim zijn maar minder ver afwijken van het gemiddelde dan zijzelf. Net zoals de leerkrachten de kinderen niet mogen inschatten op basis van hun (vermeende) kennis over de ouders, mogen ouders de verwachtingen, die zij in hun kinderen stellen, niet afstemmen op hun eigen (school)ervaringen. In veel gevallen zijn die verwachtingen immers te hoog en worden er onheuse eisen gesteld aan de kinderen.
Hoe weet men dit?De Britse psycholoog Francis Galton (een neef van Charles Darwin) was de eerste die hier onderzoek naar verrichtte en in 1888 berichtte over "Regressie naar het gemiddelde". Hij gaf zijn uitleg over "Regression towards mediocrity" in ANTHROPOLOGICAL MISCELLANEA (PDF, 1.2MB - Engels). Hij stelde vast dat verschillende menselijke eigenschappen, waaronder lengte en intelligentie, de neiging hadden om dichter bij het gemiddelde te liggen in een volgende generatie.
Dit betekent bv. dat de kinderen van uitzonderlijk grote ouders meestal groter zullen zijn dan het gemiddelde van de bevolking, maar dat de afwijking van het gemiddelde minder groot is dan bij hun ouders. Hetzelfde geldt voor uitzonderlijk kleine ouders: hun kroost zal meestal ook kleiner zijn dan het gemiddelde, maar zal niet zo ver van het gemiddelde afwijken als hun ouders. En dit geldt ook omgekeerd: ouders van heel grote kinderen zijn meestal kleiner dan hun kinderen en ouders van heel kleine kinderen zijn meestal groter dan hun kinderen (waarbij elke generatie wel met het gemiddelde van de eigen generatie vergeleken wordt). Betekent dit nu dat na enkele generaties iedereen zich dichter bij het gemiddelde zal bevinden? Helemaal niet! De reden hiervan is eenvoudig: er zijn véél meer mensen die een gemiddelde waarde van een 'eigenschap' (lengte of IQ) hebben dan er mensen zijn die een 'extreme' waarde van die eigenschap hebben. De eenvoudigste manier om te begrijpen hoe dit komt is om eens te kijken naar het aantal ouders met een bepaald IQ en het percentage kinderen met een bepaald IQ dat gemiddeld uit zo'n ouderkoppel geboren wordt. Per mens met een IQ van 130 of meer zijn er ongeveer 10 met een IQ tussen 110 en 130. Bij de ouders met IQ>130 zullen er weliswaar procentueel meer zijn die kinderen hebben met een 'hoog' IQ dan bij ouders met IQ<130, maar deze laatsten zijn in absolute aantallen met véél meer. Het resultaat op het einde van de rit is dat er in absolute cijfers véél meer kinderen met een 'hoog' IQ afkomstig zijn van ouders met een 'niet zo hoog' IQ dan met een 'hoog' IQ. Hier speelt dus de macht van het getal! Dat zal je ook duidelijk merken aan het voorbeeld dat hier volgt. Dit is bv. een tabel met de gegevens over de ouders van kinderen met een IQ van 140 of meer, een IQ dat toegekend wordt aan ongeveer 4 kinderen op 1000. Deze tabel gaat uit van een regressie van 0.6 (zie hieronder voor meer uitleg over de betekenis hiervan) en van een miljard ouderkoppels. We gaan uit van een kind voor elk koppel. De kolommen van de tabel zijn:
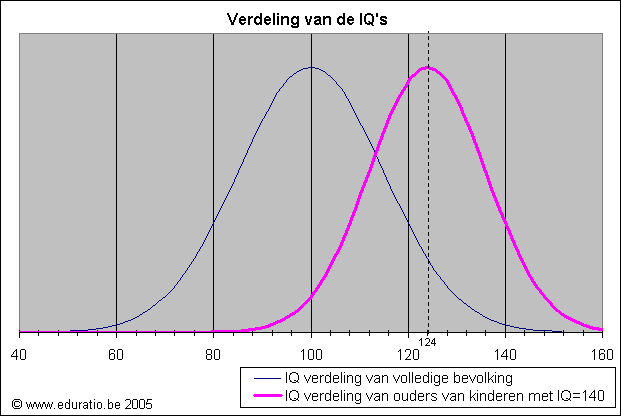
De vette getallen in de tabel zijn een voorbeeld: op een totaal aantal van een miljard ouderkoppels zijn er 161.000.000 waarvan het gemiddeld IQ tussen 110 en 119 ligt. Van hun kinderen zal 0.47% een IQ toegekend krijgen van 140 of meer. In de veronderstelling dat elk koppel één kind krijgt, zullen er dus uit deze koppels 758.000 kinderen met een IQ van 140 of meer geboren worden. Ongeveer 1 van de 5 kinderen met IQ≥140, die uit dit miljard koppels geboren zullen worden, zijn m.a.w. afkomstig van ouders met een IQ tussen 110 en 119. In elke generatie van een miljard mensen, zowel ouders als kinderen, zijn er ongeveer 3.830.000 aan wie (volgens de definitie van IQ) een IQ van 140 of meer wordt toegekend. Als je nu kijkt naar de ouderkoppels van kinderen met een IQ van 140 of meer, dan merk je dat 2.255.000 van die ouderkoppels zelf een gemiddeld IQ hebben onder de 130 (som van de eerste vier rijen van de derde kolom), terwijl 1.574.000 van die ouderkoppels zelf een IQ van 130 of meer heeft. M.a.w. 59% van de ouders van kinderen met een IQ van 140 of meer hebben zelf een IQ onder de 130. Een gelijkaardige berekening toont trouwens dat 75% van de ouders van kinderen met een IQ van 130 of meer zelf een IQ onder de 130 hebben. Merk op dat veel IQ-tests (zoals de veelgebruikte WPPSI en WISC) een laag 'plafond' hebben: dan komen de kinderen met een bepaald IQ boven het 'plafond' gewoon in een 'lagere' regio terecht. De meeste kinderen met IQ boven de 150 tref je dan bv. aan in de regio 140-149. Dit doet natuurlijk niks af aan het besluit. Hoe groot is het verschil tussen opeenvolgende generaties?Het gemiddelde kind valt terug naar ongeveer 60% van de afwijking (van het gemiddelde) van de ouder. Een praktijkvoorbeeld maakt dit duidelijk: kinderen van een ouder, die zelf een IQ 140 heeft, zullen gemiddeld IQ 124 (d.i. het gemiddelde, 100, plus 60% van de afwijking van de ouders) hebben. Kinderen van een ouder met IQ 80 zullen gemiddeld een IQ hebben van 92.Dit geldt ook omgekeerd: een ouder van een kind met IQ 150 heeft gemiddeld een IQ van 130 (hetgeen betekent dat de helft van de ouders een IQ onder de 130 heeft). Net zoals het IQ van de totale bevolking verdeeld is volgens een gausscurve met gemiddelde=100 en standaard deviatie 15, zo is het IQ van al de nakomelingen van alle mensen met IQ=150 verdeeld volgens een gausscurve met gemiddelde 130 en standaard deviatie 12. Ook het IQ van de ouders van kinderen met IQ=150 is verdeeld volgens eenzelfde gausscurve. Microsoft Excel laat toe om dit alles op vrij eenvoudige manier te berekenen. Als de cel A1 het IQ van een kind bevat, dan zal de formule 100*NORMDIST(130,100+(A1-100)*0.6,12,true) het percentage ouders met IQ lager dan 130 geven. Deze figuur toont de verdeling van de IQ's in de totale bevolking (dunne blauwe lijn) en de verdeling van de gemiddelde IQ's van de ouderkoppels van al de kinderen met IQ=140 (dikke roze lijn). Merk op dat de tweede gausscurve iets 'scherper' is: de standaard deviatie bedraagt slechts 12 i.p.v. 15, de standaard deviatie van de IQ verdeling bij de totale bevolking.
Heeft men deze regressie ooit gemeten of is dit louter theorie?Dit is niet louter theorie, dit is iets wat men meerdere keren proefondervindelijk vaststelde. Het is een feit.In de jaren twintig van de twintigste eeuw startte de Amerikaanse psycholoog Lewis Terman een longitudinaal onderzoek, waarin hij meer dan 1000 hoogbegaafde (zijnde de 1% hoogst scorende op een IQ-test) kinderen opnam (dit onderzoek loopt nog steeds verder in 2005). In 1950 testte Terman 384 nakomelingen van de ondertussen volwassen geworden kinderen uit de studie. Hij bracht hiervan verslag uit in Volume 4 (p. 236) van zijn reeks "Genetic studies of genius". De meeste kinderen van zijn hoogbegaafde studieobjecten bleken intelligenter dan gemiddeld, maar weken minder ver af van het gemiddelde dan hun ouders: uit de IQ-tests van de kinderen kwamen scores tevoorschijn die gemiddeld zo'n 24 punten onder deze van de ouders lagen.
Tien jaar later werden meer dan 1500 nakomelingen getest, de resultaten (zie Volume 5 p. 141) bevestigden de eerste bevindingen. In Development, Genetics, and Psychology beschrijft auteur Robert Plomin (p. 258) de "Hawaii Family Study of Cognition" (HFSC), een studie uitgevoerd in de jaren zeventig door John DeFries. Hierbij werden 1135 families (830 Kaukasische en 305 Japanse) bestudeerd en werden er van al de leden van de families IQ-tests afgenomen. Er werd een regressie van 0.6 gemeten. In hoofdstuk 8 van How to Use (And Misuse) Statistics (Gregory Kimble), waarin het begrip "correlatie" wordt uitgelegd, gebruikt de auteur de correlatie (en regressie) tussen 'midparent IQ' en 'offspring IQ' als illustratie. Ook hij gebruikt een regressie van 0.6 in zijn voorbeelden. Bibliografie
EduRatio wil graag de volgende mensen bedanken voor de hulp die zij boden bij het tot stand komen van dit artikel: Robert Plomin, John DeFries, James Flynn en Charles Murray. Zij gaven allen waardevolle opmerkingen en staken een handje toe bij de statistische berekeningen. Naar aanleiding van deze pagina wijdde het Nederlandse tijdschrift over hoogbegaafdheid Talent in het meinummer van 2006 een artikel aan dit onderwerp: "Hebben hoogbegaafde kinderen ook hoogbegaafde ouders?" (156KB, PDF). De uitgeverij (Koninklijke Van Gorcum BV) en de auteur (Jan te Nijenhuis) gaven ons de toelating voor opname op onze website, waarvoor dank! |
Gebruikt jouw school al het stappenplan voor leerlingen met een leervoorsprong?